May 2014 saw the market launch of the Liam F1. A lot of publicity surrounded the roll out of this new wind turbine. It weighs just around 55 kilograms (120 pounds) and it measures 1.5 meters (5 feet) in diameter.  The idea would be to ultimately put it in large numbers on roofs and on top of street lights. Individual consumers would be able to bring down their electricity bills significantly. However, with some simple high school math and physics it is easily checked that the claims are exaggerated.
The idea would be to ultimately put it in large numbers on roofs and on top of street lights. Individual consumers would be able to bring down their electricity bills significantly. However, with some simple high school math and physics it is easily checked that the claims are exaggerated.
The Liam F1 is the brain child of Marinus Mieremet and The Archimedes LLC. The company takes its name from the Greek mathematician, because its constructions are inspired by Archimedes’ screw and the Archimedean spiral.
The efficiency of a wind turbine
The shape of the turbine is presumably really new and innovative. Instead of the usual blades we have a kind of screw (see photo). But whether you are working with blades or with a screw, the principle remains the same. You slow down the wind and part of the wind’s kinetic energy is transferred to the turbine (see illustration). The amount of wind that you catch is proportional to the area that is perpendicular to the direction of the wind. That area we call A (in the illustration it says D). The wind speed v is, of course, very important. The amount of wind that hits the turbine is proportional to v and the kinetic energy of that wind is proportional to v2. All in all, there is the following formula for the maximal power Pmax, i.e. the maximal number of watts that a wind turbine can deliver:
The amount of wind that you catch is proportional to the area that is perpendicular to the direction of the wind. That area we call A (in the illustration it says D). The wind speed v is, of course, very important. The amount of wind that hits the turbine is proportional to v and the kinetic energy of that wind is proportional to v2. All in all, there is the following formula for the maximal power Pmax, i.e. the maximal number of watts that a wind turbine can deliver:
Pmax = (1/2) (16/27) ρ A v3
Here the symbol ρ (rho) represents the air density. The air density is 1.29 kg/m3 (kilograms per cubic meter). The factor 16/27, i.e. 59%, is a consequence of Betz’s Law. Without this factor the formula just gives the total amount of kinetic energy of the air that goes per second through A.
So for our calculations we can ultimately use
Pmax = 0.38 A v3 ,
where A is in square meters, v is in meters per second, and the resulting Pmax is in watts.
Wikipedia has a good derivation and explanation of this Betz’s Law. What it boils down to is that you can not completely stop the air after it goes through the turbine. If the air were to stand still behind the turbine, no new air could come through it. In the end the air behind the turbine is flowing away slower than it came in. Because of this the air in front of the turbine is slowed down and partly curved around the turbine. Already a century ago, Betz derived that maximal efficiency occurs when the air behind the turbine flows away with a third of the original wind speed v.
The above formula for Pmax gives an upper limit. It is a theoretical maximum that is actually never achieved with a real wind turbine. Betz’s derivation was based on some simple and basic principles. With the more sophisticated and modern computational fluid dynamics (CFD), the upper limit is brought down to 80% of the Betz limit. The best wind turbines operate in good agreement with CFD theory and indeed achieve about 80%. In what follows we will give the Liam F1, Mieremet, and The Archimedes all the benefit of the doubt. We assume that there are no energy losses due to friction of moving parts or heating up of the electrical wiring. Eighty percent of Pmax is what we will take as the output of the Liam F1.
On the webpage of The Archimedes there are a lot of vague statements about the “golden ratio” and “natural shapes.” But here I found some links to articles with more meaningful things like graphs and numbers. In an article written by Mieremet himself, we find a graph with measurements of the efficiency at different wind speeds. The graph shows that under optimal conditions (i.e. the best wind speed and the optimal speed of rotation of the turbine for that wind speed), the Liam F1 has an efficiency of 88%. The measurements, however, were all done in a wind tunnel and give ground for some skepticism. Measurements in a wind tunnel are unreliable when wind turbines are involved. In the above illustration we saw that the air behind the turbine moves slower. The cylinder of slower moving air behind the turbine must have a bigger diameter than the diameter of the wind turbine. The illustration to the right here makes that clear once more.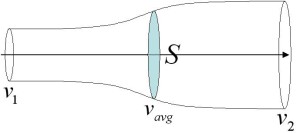 The volume of air that moves per second through a cross-sectional area equals Av, where A is the cross-sectional area and v is the speed. It is obvious that when the speed v is brought down, that the cylinder must then “fan out” to a larger area A. In the illustration, the cross-sectional area of the wind turbine is S. Betz derived that air speed at S is the average of the speeds v1 and v2.
The volume of air that moves per second through a cross-sectional area equals Av, where A is the cross-sectional area and v is the speed. It is obvious that when the speed v is brought down, that the cylinder must then “fan out” to a larger area A. In the illustration, the cross-sectional area of the wind turbine is S. Betz derived that air speed at S is the average of the speeds v1 and v2.
The fact that the cylinder of air expands behind the wind turbine is important for the interpretation of wind tunnel data. If the wind tunnel is too narrow to accommodate the “fanning out” behind the turbine, then we get a situation that no longer resembles what would happen in the open field. Air that would normally go around the turbine is then pushed through the turbine by the wind blower at the beginning of the tunnel. That Mieremet and his colleagues find the same graph for the efficiency at all speeds above 7 m/s indicates that something like that may be happening here.
Generated power at constant wind speed
Assume a constant wind speed of 4.5 m/s. We substitute this in the above formula. The device has a diameter of 1.5 m. This means A=1.77 m2. With this A, we find Pmax = 61 watts for the Betz limit. With the manufacturer’s claim that the Liam F1 operates at 80% of the Betz limit we are ultimately left with, at best, 50 watts. Fifty watts is not much on the scale of what an average household consumes. An old fashioned light bulb takes 60 watts. A microwave oven, a vacuum cleaner, and a washing machine all use 1000 watts or more. An average Dutch household consumes 0.4 kilowatt (this corresponds to 365 × 24 × 0.4 = 3500 kWh per year, i.e. about 10 kWh per day). An average American household consumes about three times as much, mostly because of the ample use of air conditioners.
Generated power at variable wind speed
The wind does not blow the entire year with exactly one speed. Wind speed varies and this leads to a complication. Because of the cubic power in the above formula, the average delivered power in the course of a year does not equal the delivered power at the average wind speed.
The graph of the cubic function f(x) = x3 is curving upward (“convex”). Because of this curving, the average of the cube (e.g. 14, the average of 13 and 33) is always larger than the cube of the average (8 = 23 in this case).
To correct for the fluctuations of the wind speed we need the distribution of the wind speed in the course of a year. An internet search quickly leads to good results. Weather stations acquire these kind of data and some weather stations put them on the internet (e.g. here). On the website of the KNMI (the Dutch National Meteorological Institute) I found a 250 page book, Windklimaat in Nederland (Wind Climate in the Netherlands), written by J. Wierenga and P.J. Rijkoort (Staatsuitgeverij, The Hague, 1983). On page 118 we see exactly the kind of graph that we need (see illustration). 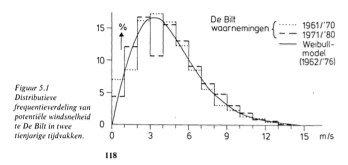 This distribution is for the city of De Bilt (where the KNMI is). The average wind speed there is 3.5 m/s. The distribution indicates how often each wind speed occurs. The so-called Weibull distribution turns out to be a good fit to the measured distribution.
This distribution is for the city of De Bilt (where the KNMI is). The average wind speed there is 3.5 m/s. The distribution indicates how often each wind speed occurs. The so-called Weibull distribution turns out to be a good fit to the measured distribution.
With the distribution it is easy to obtain the average value over a year of v3. This “new v3” is then what has to be substituted in the above equation for Pmax. One can also compare the “new v3” with the cubic power of the simple average, which we will call the “normal v3.” I did the calculation for several wind speed distributions at several locations. At best the “new v3” was twice as large as the “normal v3.” So for an average wind speed of 4.5 m/s, the Liam F1 will give an average output, not of 50 watts, but of 100 watts.
Average wind speed and average generated power are extensively covered on the British website Windpower Program. The second graph on page 16 shows that the factor two that was derived in the last paragraph is indeed a very good estimate for wind speeds of more than 4.5 m/s. For average wind speeds of 7 m/s and higher the factor is a little smaller.
Intermezzo about watt and kilowatt-hour
Watt (W) and kilowatt-hour (kWh) are often confused in discussions about energy and energy consumption. The promotion and press coverage of the Liam F1 was not immune to this confusion. On the webpage of The Archimedes we find the claim: “In the Netherlands with an average wind speed of 4.5 m/s, it will generate between 300 and 2500 kilowatts per year.” This statement is meaningless unless they mean kilowatt-hour where they write kilowatt. Many websites copy this misunderstanding and one site, for instance, even talks about “2500 kilowatt of energy per hour.”
Watts refer to power. Power is the energy that is used or generated per unit of time. Energy and power have the same relation as distance and speed. One kilowatt-hour (kWh) is the total amount of energy that is consumed in an hour by a one kilowatt device when it is turned on. It is also the energy that is delivered by a 100 watt turbine that is running for 10 hours. When you receive your electricity bill, you are charged for the number of kWh that you have used. In the Netherlands one kilowatt-hour costs about 0.23 euro. That price includes taxes, tariffs, service costs, etc. It is not difficult now to compute what an average household pays for its electricity. We saw earlier that an average household consumes about 3500 kWh per year. That leads to 0.23 (euro per kWh) times 3500 (kWh) = 805 euros for the year and about 67 euros per month.
How fast does the Liam F1 pay back for itself?
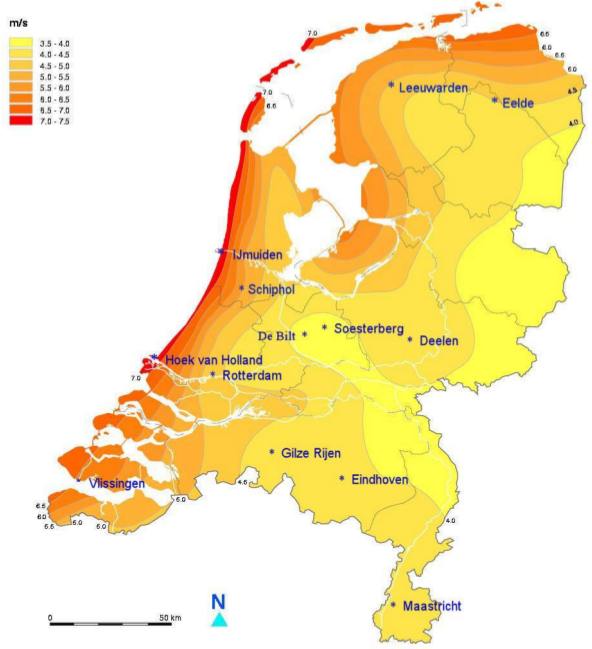
Back to the Liam F1. The illustration above is a wind map of the Netherlands (from De Klimaatatlas (The Climate Atlas), 2004, Publishing House Elmar BV). In the strip that runs through Eelde, Leeuwarden, and Rotterdam, the average wind speed is between 4.5 and 5.0 m/s. We derived earlier how the turbine generates on average 100 watts when the average wind speed is 4.5 m/s. That leads to 880 kWh when the turbine is turned on for the entire year. Assuming that the consumer can store the generated power or sell it back for 0.23 euro per kWh, the 880 kWh translates back into 200 euros per year. The Liam F1 costs 3999 euros. So it takes 20 years for the Liam F1 to earn itself back.
It should be emphasized again at this point that this estimate gives the best that is achievable. We gave the Liam F1 the benefit of the doubt with every assumption that was made.  So it is impossible for someone in Rotterdam to earn his Liam F1 back within 20 years. It is possible, however, that it will take more than 20 years.
So it is impossible for someone in Rotterdam to earn his Liam F1 back within 20 years. It is possible, however, that it will take more than 20 years.
At Schiphol, the national airport, the average wind speed is 5.17 m/s. Repeating the computation, we then find an annual yield of about 1300 kWh. Only at v = 6.4 m/s do we achieve the 2500 kWh, i.e. 575 euros, per year that the manufacturer claims. With the numbers in the table on the left, we can derive that only in IJmuiden and Hoek van Holland, two coastal towns, the Liam F1 can, in principle, earn itself back in seven years.
Inaccuracies in the brochure
There are statements in the company’s brochure about the Liam F1 that are demonstrably untrue.
We read there, for instance, “On average the Liam F1 produces approximately 1433 to 1800 kWh annually (with an estimated average wind speed of 5.2 m/sec).” Substituting 5.2 m/s into the above expression for Pmax and multiplying by 0.8 (for the efficiency) leads to 76 watts. Multiplying 76 watts first by two (for the fluctuations of the wind speed) and next by 24 times 365 (to get the annual yield), we arrive at 1325 kWh. This maximum achievable result is actually a little bit below the lower limit given in the brochure.
According to the graph on the bottom left of the first page of the same brochure the Liam F1 gives 200 watt at a constant wind speed of 6 m/s. This is impossible! With 6 m/s in the above formula for Pmax, we find 145 watts for the Betz limit. You will never exceed this limit! With an 80% efficiency one finds 116 watts. After some more searching on the company’s website, I found a poster presentation of a Korean group about the Liam F1. According to a graph on the right side of the poster (second column, second row), the output at a wind speed of 6 m/s is 120 watts. This is already a little bit more realistic. However, this was a wind tunnel result, and, as was mentioned before, wind tunnel results have to be considered with some caution.
Small urban wind turbines versus the big wind turbines
The Liam F1 is promoted as an urban wind turbine. The entire idea of an urban wind turbine is somewhat dubious. Wind farms are built out where it is flat and treeless or even in the sea or ocean. That’s not just to safeguard the population against the noise. In a flat landscape wind speeds are generally fairly constant. But as soon as this constant wind finds itself between trees and buildings, turbulence starts. Wind gusts then go in all possible directions. Furthermore, in the presence of all the obstacles, the average wind speed decreases. A turbine right up against a building as in the picture on top is a very bad idea.
The small urban wind turbine, moreover, is not a new concept. It has even been tested in the field. Numbers and graphs from British and Dutch tests are found here, here and here. The results are not very encouraging. Some of the small wind turbines did not even generate enough energy to keep up with the minimal demands of their own electronics.
In the above table we see that the coastal town of Hoek van Holland has an average wind speed of 7 m/s. This measurement, however, was taken at the weather station of the Dutch National Meteorological Institute. Their building is on top of a dune almost right off the beach. On the internet I found a small weather station in the town of Hoek van Holland itself. This non-government-associated weather station puts its data on the web. Its wind meter is located on the roof of a house. After going here and clicking on 1Y, it can be ascertained that the average wind speed on this roof is not even half of the 7 m/s at the dune. And remember again that a factor 1/2 in wind speed translates into a factor (1/2)3 = 1/8 for the generated power!!!
On the webpage about the Market Launch we find out that 7000 Liam F1s have already been ordered. That corresponds to 28 million euros. The following calculation will show that 7000 Liams are not a smart way to invest 28 million euros in wind energy.
We saw earlier that the Liam F1 has a 1.8 m2 cross section over which it catches wind. Seven thousand Liams together thus correspond to 12,600 m2. Here I found that a traditional large wind turbine with an axis at 100 meters altitude and blades of 50 meters in length costs about four million euro. So seven such giant wind turbines is what 28 million euros buy.
With a blade radius of 50 meters, one such giant wind turbine covers a wind catching area of A = 7850 m2 (= 3.14 × 50 × 50). Multiplying this number by seven, we find that the seven giant turbines cover 55,000 m2, i.e. more than four times as much area as the 7000 Liams. If efficiency and wind speed are the same, then the seven giants will give four times as much power as the 7000 Liams. However, wind speeds are not the same. At 100 m altitude the wind speed is generally 50% higher than on the ground (see, for example, here and for a comparison between wind speeds on the ground and on 100 m altitude see also here). Assuming that the average wind speed of 1.5 × v applies to the entire surface area A that is covered by the blades, we find, with the above formula for Pmax, a power that is a factor (1.5)3 = 3.4 larger. The aforementioned factor four then become a factor 4 × 3.4. And that is almost fourteen. So, compared to the Liams, the giant turbines give about fourteen times as much kWh per euro.
Conclusions
In late May and early June 2014 there was a lot of publicity around the Liam F1. Even The Washington Post devoted an article to it.
We already referred to the confused statement on the website of The Archimedes: “In the Netherlands with an average wind speed of 4.5 m/s it will generate between 300 and 2500 kilowatts per year.” Both the large populist newspaper De Telegraaf and the environmentalist publication de Groene Krant turn this into the proposition that the Liam F1 gives at 5 m/s on average 2500 kWh per year. That boils down to 285 watts. De Telegraaf writes “2500 kilowatt hour energy” and leaves out the “per year.” But they do add that this is about half of what an average household consumes. Everyone can plug 5 m/s into the above equation and deduce that a turbine with a 1.5 m diameter has an unexceedable Betz limit of 84 watts for that wind speed. But the press is cheering and appears willing to warp the facts so they can cheer louder. There is a lot of know-how about wind energy in the Netherlands and in the United Kingdom. It is a real pity that apparently no reporter took the initiative to go and talk to a real expert. De Groene Krant reports that one university professor made a critical remark to the National Broadcasting Service. This professor questioned the time in which the Liam F1 would pay back for itself. But there was no further elaboration on that assessment.
Decentralization of energy supply and energy distribution is something worth pursuing. A reliable supply of energy is the umbilical cord for modern industrial, societies. It is democratic when something so essential is taken out of the hands of captains of industry and when a private citizen can invest in the generation of his own green energy. However, in terms of kWh per euro, the giant turbines are at least an order of magnitude cheaper than the products of The Archimedes, even if all the claims about the Liam F1 are true.
The Liam F1 is not seriously competing with the giant turbines until its price goes down to about 800 euro and the warranty is extended to at least 10 years. An independent agency should, furthermore, test the Liam F1: the Liam F1 should operate in the open field for a full year right beside a wind meter. Wind speed and generated power should be recorded continuously. Only if all these conditions are met, can we start a serious discussion of the Liam F1.
The press coverage and the brochure are dishing out a pipe dream. An unavoidable disillusion awaits the buyers of the Liam F1. That really is a sad thing. It can damage the reputation of wind energy in general and it can make people lose confidence in the development towards a more decentralized production of green energy. Energy is serious business, way too serious for mindless fads.
[translated from: ‘Gebakken lucht rondom een windturbine’ published on August 16th 2014 on this site]

Now more then a year has passed and still no data about the test of the Korean University can be found on the website of the Archimedes. Nor results of worldwide field test, as the Archimedes promised in the comments of the Dutch version of this blog.
Dealer Windvoordeel has stopped selling the machines but does not explain why. The site is for sale.
http://web.archive.org/web/20160109194541/http://www.windvoordeel.nl/
They have however published some field testresults at Eemdijk, a region with 4.0-4.5m/s winds.
Even with results from a windy month like January, they could not project a total year result above 700kWh.
http://web.archive.org/web/20160109194654/http://www.windvoordeel.nl/nieuws/2015/01/1e-testresultaten-liam-f1-veldtest-eemdijk
In the mean time a new converter had to be developed wich costs 1.500 euro. Total costs including installation now amount between 8.000 and 10.000 euro.
http://houhetwarm.nl/kleine-windmolen-liam-en-zijn-omvormer/
There is not a lot of news on the Archimedis website, it seems to me they now concentrate on markets outside the Netherlands.
http://dearchimedes.com/blog/archive/
A similar article about the 2dutchwindmill would also be nice… Seems to be the new hype in windenery.
Well my reaction is that the plans should be given out to the Liam F1 and let the homeowner build them for $10 or $20 each. This way the cost would be worth the investment . it the landowner could build 5 to 10 of these and mounted them with fairly good seasonal wind, the person should be able to get his investment back and get a little profit back the same year.
But this company will never make it when trying to get their initial investment back and charging future buyers with that cost. 7000 euros a piece is outrageous for what it is. How abot 100 US dollars. Some would buy it. How about selling plans for $100 dollars along with the sales of the circuitry. Yes! There you have it, sell the idea to make the money. I will buy that. Full size plans (layout of the screw itself). Circuitry extra, Wow how much does paper cost? That’s 100%profit boys!